By Adam Thoms, Ph.D., and Nick Christians, Ph.D.
To understand the basic mathematics of irrigation, it is best to start with a few concepts related to the application of water to the surface area of the land. The first concept is that of the “acre-foot.” An acre-foot (ac-ft) of water is the amount of water required to cover one United States (US) acre (43,560 ft2) to a depth of 1 foot. This is a standard unit used by engineers and others who deal with water as part of their job.
You will see several numbers related to the acre-foot in print and on the internet. These vary slightly, depending on where in the calculation process the author rounded. The number we will use for this article is based on rounding late in the calculation, and is the one used by most engineers in the field. It is:
1 ac-ft = 325,851.4 gal.
A clear understanding of the ac-ft is key to understanding the calculations that follow, so take a minute and imagine in your mind an acre of land covered by one foot (12 inches) of water.
If I have an area of five acres to irrigate, and I were to apply one foot of water to each acre, a total of
(5 ac)(325,851.4 gal.) = 1,629,257 gal. of water
would be required to make that application.
A second concept that will be useful in irrigation calculations is the acre-inch. This is the amount of water required to apply one inch of water to an area of 43,560 ft2. This is calculated by dividing the number of gallons in an ac-ft by 12 inches in a ft.
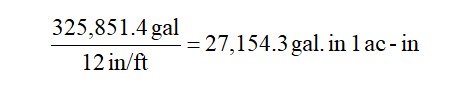
This number will be very useful in calculating irrigation needs.
For example, your sports complex totals 12 acres of irrigated fields. How much water would be required to irrigate those fields during one week with the equivalent of 1 inch of water? There are 12 ac, and each acre receives 1 in of water (27,154.3 gal). Therefore,
(12 ac) x (27,154.3 gal/ac-in) = 325,851.4
a total of 325,851.4 gal of water would be required for the application.
Now, let’s consider a budgeting question. The sports complex buys water from the city at a rate of $.03/cubic foot (ft3). You are asked to calculate how much water must be purchased to irrigate the 12 ac of fields with 1 in of water per week for an 8-week period during a drought and give the city an estimate of the cost.
If one week requires 325,851.4 gal., then 8 weeks would require
325,851.4 x 8 = 2,606,811.2 gal.
Another useful concept for making these calculations is the number of gallons in a ft3 of water. That conversion factor is 7.480519 gal/ft3. Therefore, you will need:
2,606,811.2 gal/7,480519 gal/ft3 = 348,480 ft3
If each ft3 cost $.03, then:
348,480 ft3 x .03/ft3 = $10,454.40
You would need to budget $10,454.40 for water for these fields. (Hopefully it will rain, and you will not need it all).
Now let’s turn things around and assume that you have a lake on the property from which you can draw irrigation water. The lake is 3 surface acres and averages 4 feet deep. Disregarding evaporation, how many weeks could you irrigate the 12 acres of fields at 1 in of irrigation water per week.
The lake is 3 acres in surface area and averages 4 ft in depth, therefore it contains:
3 ac x 4 ft deep = 12 ac-ft
12 ac-ft x 325,851.4 gal/ac-ft = 3,910,216.8 gal.
If there are 3,910,216.8 gal. in the lake, and you are going to use 325,851.4 gal. for each week of watering, you could water:
3,910,216.8 gal/325,851.4 gal/wk = 12 wk
You could water the 12 ac of sports fields at 1 in/wk for 12 weeks from the lake.
Again, this did not take into account evaporation or rainfall, which would affect the results, but it does give you a reasonably good number to work with for budgeting purposes.
If you are constructing a new site, you may need to figure out what your initial irrigation system can apply. If there is no existing flow rate, you will have to use an assumed flow formula.
Assumed flow takes into account a few variables to figure out how many gallons per minute are needed:
ETO – Reference evapotranspiration rate in inches per date for the crop that you are growing. In this case, it would be the turfgrass present. These often range from 0.15 to 0.50 inches per day, depending on the weather conditions. These can often be found online from various sites.
Area – You also need to know how much area you are going to water (often called the hydrozone) in square feet. For many athletic complexes, you can figure this with a simple length-by-width measurement in feet being covered by irrigation.
KC – The crop coefficient is used to help modify the reference evapotranspiration to represent the water use rate of a specific plant. Cool-season turfgrasses – such as Kentucky bluegrass, tall fescue, and perennial ryegrasses – have a normal crop coefficient 0.80 with a minimum of 0.65, while the warm-season grasses – such as bermudagrass, seashore paspalum and zoysiagrass – have a normal crop coefficient of 0.60 with a minimum of 0.35. Like the ET, these can be found online.
DU– Distribution Uniformity (%) this value will always be less than 1.0, as that is a perfect distribution and is unobtainable.
Hrs. Available – Amount of time available for irrigation to run in hours.
Assumed flow in gpm = (0.014 x ETO x Area x KC) / (DU x Hrs. Available)
This information can help you decide on many of the design components needed to help ensure adequate water is provided to the valves and heads for a fully functional irrigation system. When you specify any component for an irrigation system you need to make sure it will handle the needed assumed flow. Any component in the system that will not handle the assumed flow will now limit the flow of the system from that point on, this can include things like the water meter, service lines, and valves. Make sure to regularly check friction loss charts for pipes, as well to make sure that water velocities do not exceed 7.5 feet per second.
You can also find precipitation rates or the amount of water being applied over an amount of time for a total area fairly easily.
PR = Precipitation rate amount of water (inches per hour).
96.3 = Conversion constant, which is 1.60 if you are dealing with a flow in gallons per hour and not gallons per minute.
gpm = Flow from all irrigation heads in the area or zone should be in gallons per minute.
Total Area = Size of area or zone in square feet.
PR = (96.3 x gpm) / Total Area
This will give an idea of how much water you can apply over an area.
Finally, we can also figure out how long to run a station.
Station Run Time = (Total weekly water needs in inches per week x 60 minutes in an hour)/ (precipitation rate in inches per hour) then divide by number of days that water can be applied per week.
Here is an example:
Want to apply 1.0 inch of water per week.
Can water 4 days per week.
Precipitation rate in inches per hour is 1.3 inches per hour.
Station Run Time = (1.0 inches per week x 60 minutes per hour)/1.3 inches per hour = 46 minutes of run time needed per week.
Station Run Time = 46 min. run time per week / 4 days of watering = 11.5 minutes of watering per day or run.
One thing to keep in mind while you are figuring how long you should water: Do not apply water quicker than the rootzone will allow infiltration. If you apply quicker, the water will run off.
These basic mathematical equations can ensure that there is enough water present to properly water your athletic fields in the amount of time that you have available. This will also allow you to better use, repair and expand your irrigation systems.
Adam Thoms, Ph.D., is assistant professor specializing in commercial turfgrass management, Iowa State University, Department of Horticulture, Ames, Iowa.
Nick Christians, Ph.D., is university professor of turfgrass management, Iowa State University, Department of Horticulture, Ames, Iowa.


